Nios 10th Maths (211) English Medium Solved Assignment TMA 2024-25

Maths (211)

Tutor Marked Assignment

20% Marks Of Theory

 1. Answer any one of the following questions in about 40-60 words.

(b) (i) How many rational numbers and irrational numbers exist between the natural numbers 1 and 2?

(ii) There is/are natural number ‘n’ such that √𝑛 lies between 1 and 2. How many value(s) of n are possible? Represent √𝑛 on a real number line for each such value of n, satisfying above condition.

Answer: (i) Between the natural numbers 1 and 2, there are:

1. Infinitely many rational numbers: Rational numbers are numbers that can be expressed as the ratio of two integers. For example, numbers like 3/2, 5/4, and 7/6 are rational numbers between 1 and 2. Since you can always find a rational number between any two rational numbers, there are infinitely many rational numbers between 1 and 2.

2. Infinitely many irrational numbers: Irrational numbers are numbers that cannot be expressed as a simple fraction of two integers. Examples include V2, π (truncated), and certain non-repeating decimals like 1.414213.... Since irrational numbers also exist between any two rational numbers, there are infinitely many irrational numbers between 1 and 2 as well.

Thus, both rational and irrational numbers are infinite in quantity between 1 and 2.

(ii) We are looking for natural number(s) n such that:

1 <√n<2

Step 1: Square both sides to eliminate the square root.

1² < n < 2²

1 < n < 4

Step 2: Identify natural numbers that satisfy the inequality.

The natural numbers that satisfy 1 < n < 4 are:

n = 2, 3

Step 3: Representing sqrt(n) on the real number line:

For n = 2 √2 ≈ 1.414 so plot it between 1 and 2 on the real number line.

For n = 2 √3 ≈ 1.732 so plot it between 1 and 2 on the real number line.

Thus, there are two values of n (i.e., 2 and 3) where √n lies between 1 and 2.

2. Answer any one of the following questions in about 40-60 words.

(a) A polygon which has equal sides and equal angles is called a regular polygon. It is found that the interior angle of regular polygon having n sides can be calculated as:

Interior angle =((n-2)/2)×180°

(i) Name the simplest regular polygon and write the value of its interior angle.

(ii) Prove that the sum of the (interior) angles of a hexagon is 720°

Answer: (i)

• The simplest regular polygon is an equilateral triangle, which has 3 sides.
• Using the formula for the interior angle of a regular polygon:

So, the interior angle of an equilateral triangle is 60 degrees.

(ii) 

• For a hexagon, n = 6 (since it has 6 sides).
• The sum of the interior angles of any polygon is given by:

Sum of interior angles = (n - 2) × 180°

Substitute n = 6:

Sum of interior angles = (6 - 2) × 180° = 4 × 180° = 720°

Thus, the sum of the interior angles of a hexagon is 720 degrees

3. Answer any one of the following questions in about 40-60 words.

(b) If ABC is an equilateral triangle and AD is the median. Prove that 3AB²

 = 4AD²

Answer: To prove that in an equilateral triangle ABC, where AD is the median, the relationship 3AB² = 4AD² holds, follow these steps:

Given: 

3AB² = 4AD²

Proof:

1. Coordinate Setup: Let’s place the triangle on the coordinate plane. Set Point A at (0,h), B at (-a/2,0), and C at (a/2,0), where a is the length of each side of the equilateral triangle, and h is the height of the triangle,

2. Calculate Heighth h: The height ℎ of an equilateral triangle can be found using the Pythagorean theorem in triangle ABD, where BD=a/2 and AB=a:

AB² = AD² + BD²

But from geometry, the height ℎ of an equilateral triangle is:

h = √3/2 a

3. Length of Median AD: The length of the median in an equilateral triangle can also be derived using the properties of the triangle. We know:

AD=√3/2 a

4. Use of Pythagoras Theorem: In triangle ABD, apply the Pythagorean theorem: 

AB² = AD² + BD²

Substituting BD = a/2: 

Now, multiply the equation by 4:

4AB² = 4AD² +a²

Since AB=a,we substitute AB² = a²:

4AB² = 4AD² + AB²

Rearranging gives:

3AB² = 4AD²

Thus, we have proven that 3AB² = 4AD²

4. Answer any one of the following questions in about 100-150 words.

(a) (i) If the sum of the exponents of the prime factors in the prime factorisation of 31752 is a and the product of the exponents of the prime factors in the prime factorisation of 21168 is b. Find a:b.

(ii) Aman and Neha, donated Rs. x and Rs. y respectively from their pocket money, towards Prime Minister's National Relief Fund (PMNRF). The donations made by them are represented by the following equation:

(3-2√5)/(3+√5)=x-√5 y

Find the total donation made by Aman and Neha towards PMNRF.

Answer: (i) Prime Factorization Problem:

 We need to find the ratio a:b, where:

• 𝑎 is the sum of the exponents of the prime factors of 31752.
• 𝑏 is the product of the exponents of the prime factors of 21168.

Prime factorization of 31752:

Let's find the prime factors of 31752.

31752 ÷ 2 = 15876

15876 ÷ 2 = 7938

7938 ÷ 2 = 3969 (odd number, so not divisible by 2 anymore)

3969 ÷ 3 = 1323

1323 ÷ 3 = 441

441 ÷ 3 = 147

147 ÷ 3 = 49

49 ÷ 7 = 7

7 ÷ 7 = 1

So, the prime factorization of 31752 = 2³ × 3⁴ × 7².

The product of the exponents (for b) is:

B = 4 × 4 × 2 = 32

Thus, the ratio a : b is:

a : b = 9 : 32

(ii) Donation Equation Problem

We are give the equation:

(3 - 2 √5)/(3 + √5) = x - √5 y

We need to simplify the left-hand side (LHS) and then solve for 𝑥 and 𝑦.

Simplifying the LHS:

To simplify the LHS, we can multiply the numerator and denominator by the conjugate of the denominator (3 − 5):

First, let's simplify the denominator:

(3 + √5)(3 - √5) = 3² - (√5)² = 9 - 5 = 4

Now, simplify the numerator:

(3 - 2√5)(3 - √5) = 3(3) - 3(√5) - 2√5(3) + 2√5(√5) = 9 - 3√5 - 6√5 + 2 × 5 = 9 - 9√5 + 10 = 19 - 9√5

So the LHS becomes:

(19 - 9√5)/4 = 19/4 - (9√5)/4

Thus, we have: 

Final Answer:

1. a ∶ b = 9 ∶ 32

2. The total donation made by Aman and Neha is Rs.7.

5. Answer any one of the following questions in about 100-150 words.

(b) In a circle of radius 17 cm and centre O, PQ and RS are two parallel chords such that PQ = 16 cm and RS = 30 cm. Find the distance between the chords if

(a) The chords are on the same side of the centre of the circle.

(b) The chords are on the opposite sides of the centre of the circle.

Answer:

Given:

• Radius of the circle = 17 cm
• PQ = 16 cm
• RS = 30 cm

To Find:

• Distance between PQ and RS in both cases (a) and (b)

Solution:

(a) Chords on the same side

• Let the perpendicular distance from the center O to PQ be h1, and to RS be h2.

• Since PQ and RS are parallel, h1 and h2 are equal.

• We have right triangles OPQ and ORS.

• Using the Pythagorean theorem:

• OP² = OQ² + PQ²/4

• OR² = OS² + RS²/4

• Since OP = OR = radius = 17 cm:

• 17² = OQ² + 16²/4

• 17² = OS² + 30²/4

• Solving for OQ and OS:

• OQ = √(17² - 16²/4) = 15 cm

• OS = √(17² - 30²/4) = 7 cm

• Therefore, the distance between PQ and RS is:

• h1 + h2 = OQ - OS = 15 cm - 7 cm = 8 cm

(b) Chords on opposite sides

• In this case, the distance between PQ and RS is simply the sum of their perpendicular distances from the center.

• So, the distance between PQ and RS is:

• h1 + h2 = OQ + OS = 15 cm + 7 cm = 22 cm

Therefore, the distance between the chords is:

• 8 cm if they are on the same side of the center.

• 22 cm if they are on opposite sides of the center.

6. Prepare any one project out of the given below.

(b) Shown below is the histogram representing the runs scored by a cricket team in different overs. Answer the following questions based on the histogram.

(i) In which interval of overs the cricket team scored maximum runs?

(ii) In which intervals of overs the cricket team scored equal number of runs?

(iii) Construct a grouped frequency table for the data using equal class sizes from the above histogram.

(iv) Also construct a cumulative frequency table for the above grouped data.

(v) Construct a frequency polygon for the data.

Answer: (i) The cricket team scored the maximum runs in the interval 30-40 overs, with 70 runs.

Answer: (ii) The intervals 10-20 overs and 40-50 overs each had 50 runs scored.

Answer: (iii) Grouped Frequency Table (Equal Class Sizes)

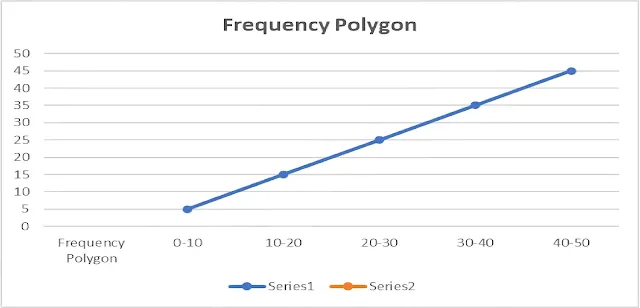
Answer: (iv) Cumulative Frequency Table

Answer: (v) Frequency Polygon

To construct a frequency polygon:

1. Use the midpoints of each interval for the x-axis.

2. Plot the runs scored for each midpoint on the y-axis.

3. Connect the points to form the polygon

Midpoints for the intervals:

• 0 - 10 --> Midpoint: 5

• 10 - 20 --> Midpoint: 15

• 20 - 30 --> Midpoint: 25

• 30 - 40 --> Midpoint: 35

• 40 - 50 --> Midpoint: 45

These midpoints (x-values) can then be plotted against their corresponding runs scored.